在考查光学显微镜的分辨率时,大部分关注点放在垂直于光轴的平面中的点对点横向分辨率(图 1)。分辨率的另一个重要方面是物镜的轴向(或纵向)分辨率,它是平行于光轴测量的,通常称为景深。
图1 景深范围

轴向分辨率与水平分辨率一样,仅由物镜的数值孔径决定(图 2),目镜仅放大细节并投影到中间图像平面。就像在经典摄影中一样,景深由最近对焦的物体平面到同时对焦的最远平面的距离决定。在显微镜下,景深非常短,通常以微米为单位进行测量。术语“焦深”指的是图像空间,通常与景深(指物体空间)互换使用。
图2 景深和数值孔径
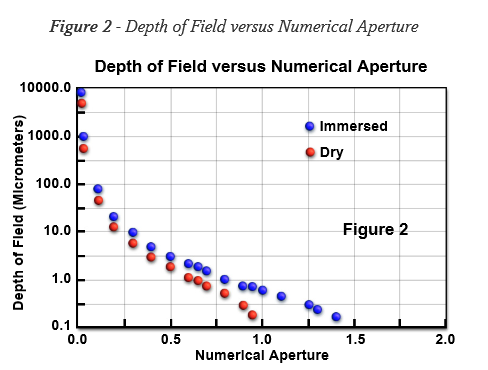
这种命名法的互换会导致混淆,尤其是当这两个术语都专门用于表示显微镜物镜中的景深时。几何图像平面可能会代表样品的无限薄部分,但即使没有像差,每个图像点也会扩展为在该平面上方和下方延伸的衍射图。艾里斑是显微镜物镜产生的衍射图案的基本单位,代表通过中间图像平面中心的截面。这增加了通过稍微不同的样本平面的 Z 轴艾里斑强度分布的有效聚焦深度。
表1 景深和焦深
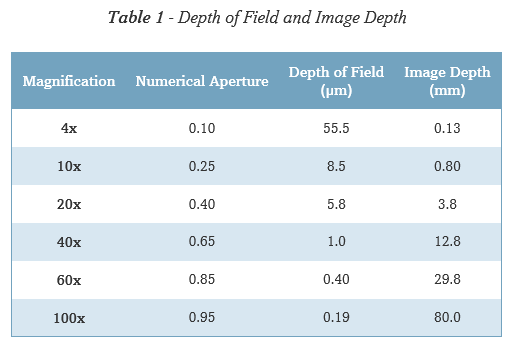
焦深随数值孔径和物镜放大倍数而变化,在某些条件下,高数值孔径系统(通常具有更高的放大倍数)比低数值孔径系统具有更深的焦深,即使景深更小(见表 1)。这在显微摄影中尤为重要,因为胶片乳剂或数码相机传感器必须在聚焦区域内的平面内曝光或照明。在高放大倍率下聚焦所产生的小错误并不像在非常低的放大倍率物镜下所产生的错误那么严重。表1 显示了随着数值孔径和放大倍数的增加,一系列物镜中景深和中间图像平面中图像深度的计算变化。
在显微镜的高数值孔径下,景深主要由波动光学决定,而在低数值孔径下,几何光学弥散圈占主导地位。使用各种不同的标准来确定图像何时变得不可接受,几位作者提出了不同的公式来描述显微镜中的景深。总景深由波和几何光学景深之和给出:
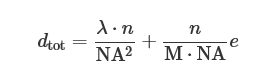
其中 d(tot) 表示景深,λ 是照明光的波长,n 是盖玻片和物镜前透镜之间的介质(通常是空气(1.000) 或浸油 (1.515))的折射率, NA 等于物镜数值孔径。变量 e 是放置在显微镜物镜图像平面中的检测器可以解析的最小距离,其横向放大倍数为M。使用此方程,景深 (d(tot)) 和波长 (λ)必须用类似的单位表示。例如,如果 d(tot) 以微米为单位计算,则 λ 也必须以微米为单位(700 纳米红光在方程中输入为0.7 微米)。请注意,衍射极限景深(方程中的第一项)与数值孔径的平方成反比缩小,而分辨率的横向极限以与数值孔径的一阶幂成反比的方式减小.因此,与显微镜的横向分辨率相比,系统数值孔径对光学截面的轴向分辨率和厚度的影响要大得多。

人眼通常可以适应从无限远到大约 25 厘米的范围,因此当人们通过目镜观察显微镜图像时,景深可以远大于上式给出的景深。另一方面,视频传感器或感光乳剂位于一个薄的固定平面中,因此使用这些传感器的景深和轴向分辨率由等式中的参数给出。在这些情况下,轴向分辨率按惯例定义为沿物镜产生的三维衍射图像轴的第一个最小值之间的距离的四分之一,在焦点上方和下方。
这些景深值和三维衍射图案中的强度分布是针对聚光镜数值孔径大于或等于物镜数值孔径的非相干照明(或发射)点源计算的。一般来说,随着照明相干性的增加(当聚光器数值孔径接近零时),景深会增加到2 倍。然而,当孔径函数不均匀时,具有部分相干照明的三维点扩散函数 (PSF) 可能会呈现复杂的方式而与目前讨论的不同。在许多基于相位的、产生对比度的显微镜模式中,景深可能出乎意料地比从上面的方程预测的要浅,并且可能会产生极薄的光学切片。
在数字和视频显微镜中,检测器或CCD 目标中的浅焦平面、在高倍物镜和高聚光器数值孔径下可实现的高对比度以及在显视器上显示的图像的高放大率都有助于减少景深。因此,通过视频,我们可以获得非常清晰和薄的光学切片,并且可以非常高精度地定义薄样品的焦平面。


